
If you’re a Class 10 student preparing for your exams, you’re likely to come across questions related to a number system conversion. Here is the Complete Number of System Conversion Questions. Understanding how to convert numbers from one system to another is an essential skill, and it can be challenging to grasp at first. In this article, we’ll cover the complete number system conversion questions that you might encounter in your Class 10 exams. By the end of this article, you’ll have a solid understanding of how to convert numbers between different number systems.
Before we dive into the questions, let’s start with a brief introduction to number systems. A number system is a way of representing numbers using symbols or digits. The most commonly used number systems are the decimal, binary, octal, and hexadecimal systems. In the decimal system, we use 10 digits (0 to 9) to represent numbers. In the binary system, we use 2 digits (0 and 1), in the octal system, we use 8 digits (0 to 7), and in the hexadecimal system, we use 16 digits (0 to 9 and A to F).
(10.25)10
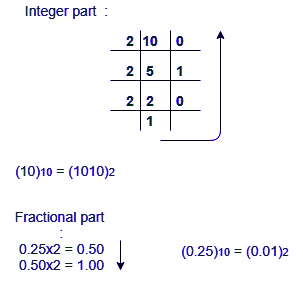
Note: Keep multiplying the fractional part with 2 until the decimal part 0.00 is obtained.
(0.25)10 = (0.01)2
Answer: (10.25)10 = (1010.01)2
(1010.01)2
= 1×23 + 0x22 + 1×21+ 0x20 + 0x2 -1 + 1×2 -2
= 8+0+2+0+0+0.25
= 10.25 (1010.01)2
= (10.25)10
(10.25)10
(10)10 = (12)8
Fractional part:
0.25 x 8 = 2.00
Note: Keep multiplying the fractional part with 8 until the decimal part .00 is obtained.
(.25)10 = (.2)8
Answer: (10.25)10 = (12.2)8
4. Octal to Decimal
(12.2)8
=1 x 81 + 2 x 80 +2 x 8-1
= 8+2+0.25
= 10.25 (12.2)8
= (10.25)10
To convert from Hexadecimal to Binary, write the 4-bit binary equivalent of hexadecimal.

(3A)16 = (00111010)2
To convert from Binary to Hexadecimal, start grouping the bits in groups of 4 from the right end and write the equivalent hexadecimal for the 4-bit binary. Add extras 0’s on the left to adjust the groups.
1111011011
0011 1101 1011
(0011 1101 1011 )2 = (3DB)16